In popular imagination, Albert Einstein is supposed to have called compound interest as the eighth wonder of the world. He did not say any such thing. Nevertheless, compounding indeed is very beneficial for your financial health. This short post provides a few ways to visualize the effect of compounding.
First, the formulae
Simple interest is calculated on the ‘principal’ – the original amount of investment. If simple interest accrues over multiple periods, it would always be calculated on the original amount of the investment. Simple Interest = Principal (P) x Interest rate per period (r) x Number of periods (n) This is an easy concept to understand.
Per Investopedia, “Compound interest is calculated on the principal amount and also on the accumulated interest of previous periods, and can thus be regarded as “interest on interest.” Compound Interest = P [(1 + r)n – 1], using the same variables as before. It is easy to notice that the multiplication operation in simple interest has been replaced by the exponential operation.
In a simple interest scenario, increasing ‘r’ or increasing ‘n’ has a linear effect on the value of interest. i.e a 10% increase in either quantity would increase the final interest by 10%. In the compound interest scenario, a 10% increase in either would have a larger than 10% effect on the final interest. We would see this visually.
Growth of a lump sum investment
For the period of 1 year, the effect is linear in compounding – as expected since the exponent is 1. Beyond that, the effect is significant. For a period of 25 years, tripling of rate – from 4% to 12% – makes the final corpus more than six times larger.
If you look down one column, say 10%, the interest for 10 years is 1.7 lacs. If you hold the investment for another 10 years, the interest almost quadruples to 6.33 lacs. All the advice that you get about starting to invest early stems from this.
Breaking down the mechanics
We have seen that compounding happens because of the interest on interest. For the 1 lac scenario above, the interest calculations for 10% look like this:
| Year | Principal | Interest on principal | Interest on Interest | |
| 1 | 1,00,000 | 10,000 | – | |
| 2 | 1,00,000 | 10,000 | 1,000 | |
| 3 | 1,00,000 | 10,000 | 2,100 | |
| 4 | 1,00,000 | 10,000 | 3,310 | |
| 5 | 1,00,000 | 10,000 | 4,641 | |
| 6 | 1,00,000 | 10,000 | 6,105 | |
| 7 | 1,00,000 | 10,000 | 7,716 | |
| 8 | 1,00,000 | 10,000 | 9,487 | |
| 9 | 1,00,000 | 10,000 | 11,436 | |
| 10 | 1,00,000 | 10,000 | 13,579 | |
| 11 | 1,00,000 | 10,000 | 15,937 | |
| 12 | 1,00,000 | 10,000 | 18,531 | |
|
1,00,000 | 10,000 | 21,384 | |
| 14 | 1,00,000 | 10,000 | 24,523 | |
| 15 | 1,00,000 | 10,000 | 27,975 | |
| 16 | 1,00,000 | 10,000 | 31,772 | |
| 17 | 1,00,000 | 10,000 | 35,950 | |
| 18 | 1,00,000 | 10,000 | 40,545 | |
| 19 | 1,00,000 | 10,000 | 45,599 | |
| 20 | 1,00,000 | 10,000 | 51,159 | |
| 21 | 1,00,000 | 10,000 | 57,275 | |
| 22 | 1,00,000 | 10,000 | 64,002 | |
| 23 | 1,00,000 | 10,000 | 71,403 | |
| 24 | 1,00,000 | 10,000 | 79,543 | |
| 25 | 1,00,000 | 10,000 | 88,497 |
The interest on principal stays constant as the principal is constant. The interest however is accumulated every year; the interest on interest thus keeps growing. In the ninth year, the interest on interest becomes larger than interest on the principal. This is one inflection point in compounding. In the 14th year, the accumulated interest on interest begins to exceed the accumulated interest on principal. This is the second inflection point. The inflection points would of course occur at different times for different interest (return) rates.
Visualizing Interest on Interest
The visual effect of the non-linear growth of interest on interest can be quite striking.
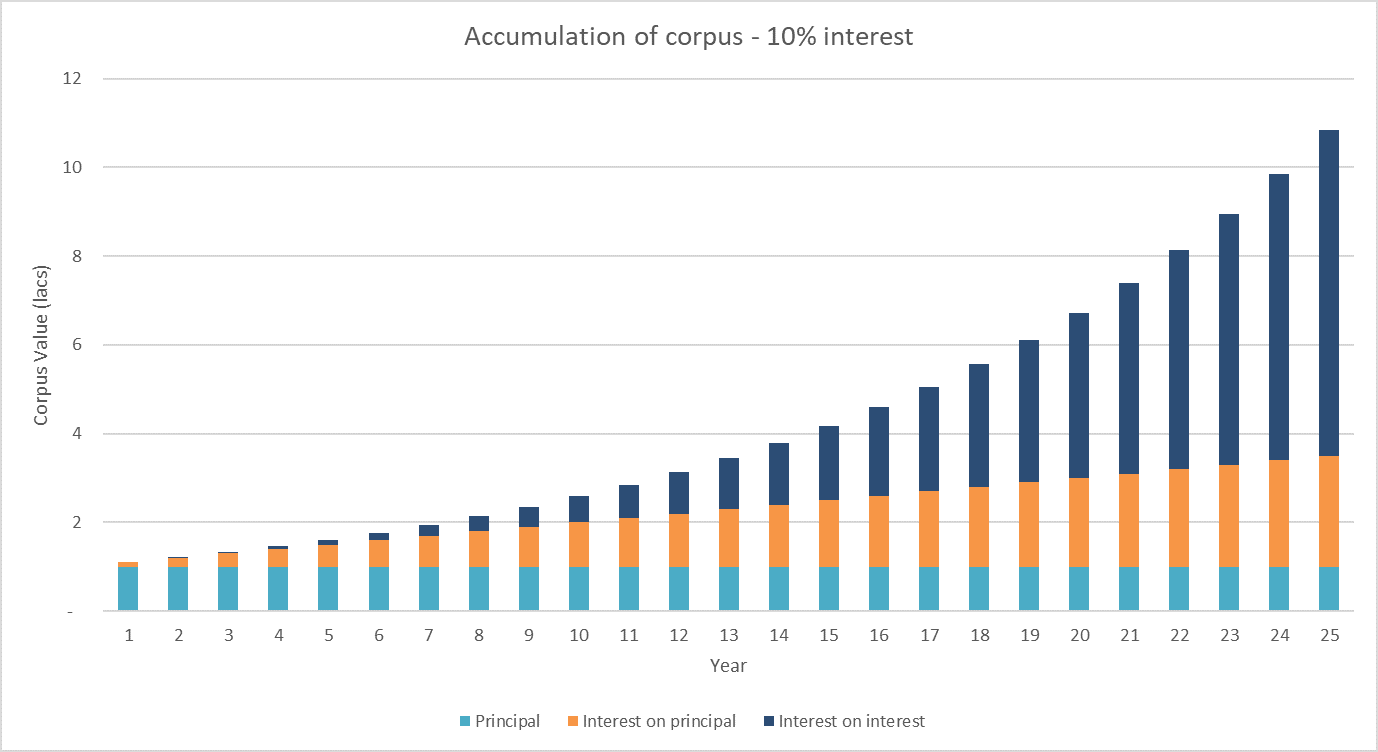
The top, purple, bar starts off small and grows in an exponential way. In the final corpus after 25 years, the interest on interest forms more than 70%; the simple interest forms just about 20%. Since this is a single investment, the principal bar stays flat, and the interest bar grows linearly.
It is also easy to see from the picture the importance of long investment horizon. The purple bar gets progressively bigger and bigger.
Impact of rate of return
We so far looked at a specific rate of return for a number of years. Let us look at a typical investor situation. One invests a small amount, say Rs 1000, every month in a product that provides monthly compounding. i.e. the interest is calculated monthly and added to the corpus. This further enhances the benefit of compounding. We look at the overall composition of the corpus with different rates of return.
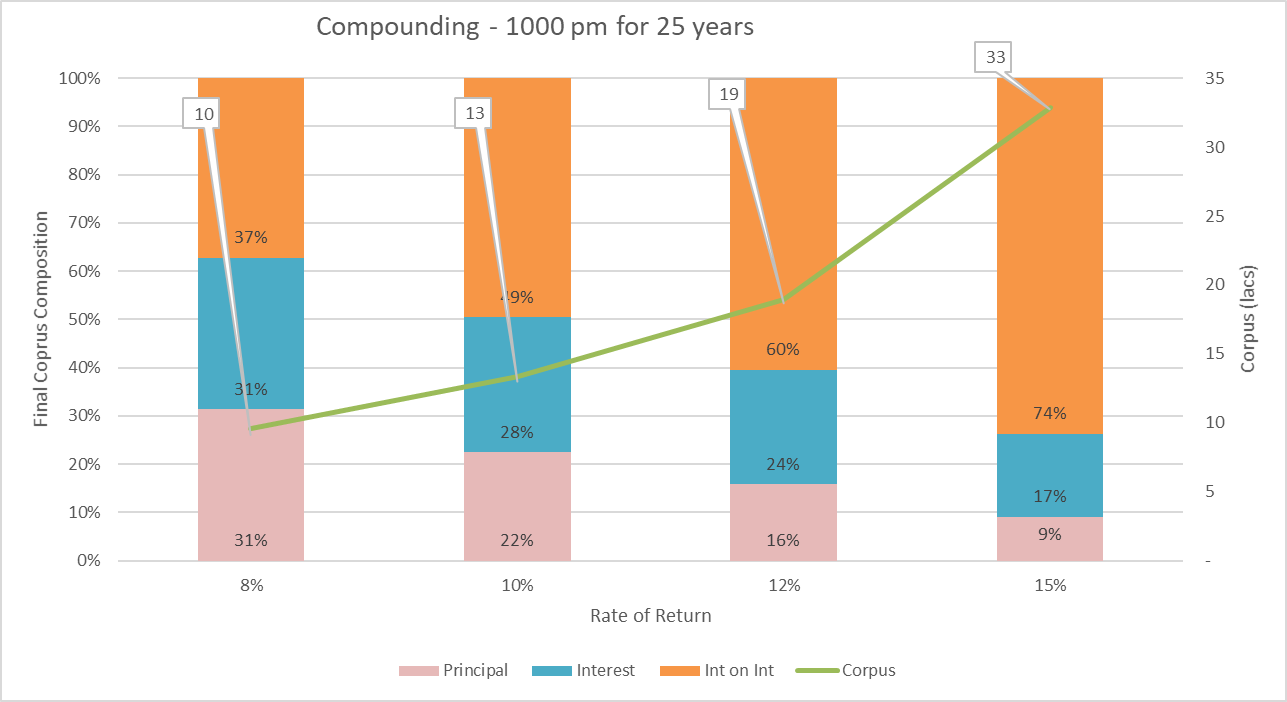
In a regular investment scenario like the above, the inflection points occur later than those for the lumpsum investment. However, the effects of increase in either the period or the rate of return are similar. A 50% increase in return – from 8% to 12% – more than doubles the overall interest – from 7 lacs to 16 lacs.
A note on CAGR
To visualize the effect of compounding, it is simpler to think of a fixed income instrument – say a Recurring Deposit. Here the rate of return (interest rate) is fixed and we can use that rate throughout the return. However, these instruments don’t give high returns like equity products. Equity returns are lumpy – they are not uniform through the tenure. To make the comparison between different products easier, the CAGR is used.
Per Investopedia, “Compound annual growth rate, or CAGR, is the mean annual growth rate of an investment over a specified period of time longer than one year. It represents one of the most accurate ways to calculate and determine returns for individual assets, investment portfolios and anything that can rise or fall in value over time.” Often equity products, particularly equity mutual funds, are perceived as compounding – this is not strictly true. Equity grows and can grow quite well. It does not really compound. However, to visualize the growth, you can use the compounding illustration.
